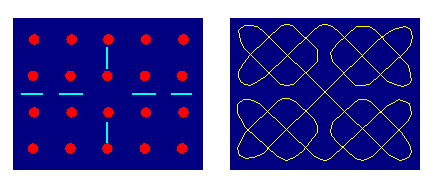
Figure 6: Example of a Celtic knot design as a mirror curve.
Properties and classes of mirror curves are analysed
by Gerdes (1990,
1993-94, chap. 4-8)
and by Jablan (1995),
who also establishes links with the theory of cellular automata,
Polya's enumeration theory, combinatorial geometry, topology, and knot theory.